*
I frequently need to find an arc of a circle when laying out walls or ceiling details. The plans will specify a radius going into the hundreds of feet but I might only need a small portion of the complete circle for my layout.Without using a centerpoint and long tape measure to physically layouton the floor;most times this is impractical because of obstructions; is it possible to find the arc given the length of the radius?
Discussion Forum
Discussion Forum
Up Next
Video Shorts
Featured Story
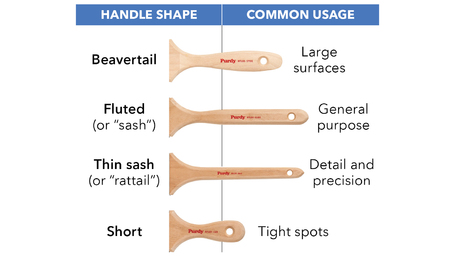
Tips for picking the right paintbrush based on paint type, surface, and personal comfort.
Featured Video
How to Install Exterior Window TrimHighlights
"I have learned so much thanks to the searchable articles on the FHB website. I can confidently say that I expect to be a life-long subscriber." - M.K.
Fine Homebuilding Magazine
- Home Group
- Antique Trader
- Arts & Crafts Homes
- Bank Note Reporter
- Cabin Life
- Cuisine at Home
- Fine Gardening
- Fine Woodworking
- Green Building Advisor
- Garden Gate
- Horticulture
- Keep Craft Alive
- Log Home Living
- Military Trader/Vehicles
- Numismatic News
- Numismaster
- Old Cars Weekly
- Old House Journal
- Period Homes
- Popular Woodworking
- Script
- ShopNotes
- Sports Collectors Digest
- Threads
- Timber Home Living
- Traditional Building
- Woodsmith
- World Coin News
- Writer's Digest


















Replies
*
Chris,
View Image
© 1999-2000
"The first step towards vice is to shroud innocent actions in mystery, and whoever likes to conceal something sooner or later has reason to conceal it."
Aristotle
*Well.. sounds like a bit of a challenge. The only thing I can think of, would be to use a template. You said "hundreds of feet" wow, that's a big arc. I'm not used to dealing with arcs on such a grand scale. But I think that if you were to mark out and cut a template on plywood, using the conventional method.(I guess you need a really long tape-I dunno,lol) You should be able to make it as large or small as you need it. So long as you can establish some reference points to place your template in. I've only been working as a framer for 3 years, so perhaps some more experienced carpenters out there will have some better ideas. If not, I hope my idea will work.. good luck
*Chris,
View Image © 1999-2000"The first step towards vice is to shroud innocent actions in mystery, and whoever likes to conceal something sooner or later has reason to conceal it." Aristotle
*Chris,
View Image © 1999-2000"The first step towards vice is to shroud innocent actions in mystery, and whoever likes to conceal something sooner or later has reason to conceal it." Aristotle
*I didn't audit your figures; but, the methodology is certainly sound; however, depending on the actually radius and length of chord, may be tough to accurately layout. If you have a plotting program, then you can plot values of a full-sized arc and a chord that is parallel to either of the axis and then caculate the chord-arc displacement: a chalk-line on the floor, a dry-wall tee-square, and a tape measure will reproduce the results in the field.
*This reminds me a little of a job we did about 8 years ago. ( not one that I care to recall )The design called for a wall with an "S" bend. To top it off it was a an external load bearing wall and it had an internal staircase running up the inside. This meant that the top plate ran from about 9 foot at one end of the "S", to about 20 foot the other.Now before you get all excited that I'm going to give you some magic math formular that we used....just settle down. We are just dumb carpenters.....so we called up the local lumber yard and got the use of their wharehouse floor to chalk out the S radii, then cut the bottom plates out of thick ply. Because the radii were so large, we had the Architect crunch some numbers on CAD for us. He was able to give us the chord measurement, then from this he gave us perpindicular measurements at 18" centers. We then faired the arcs off these.The top plates, because of the two height differances were another matter. We scratched our head for half a day, then finally just started building the damn thing in the air, got the Architect to plot and give us individual stud lengths, nailed plumbed and braced each stud into position, then cut a wide flexible piece of ply and temporary tacked it on to the top of the studs to use it as a template to mark out thicker ply for the laminated plates.The rafters?...well that's another story....
*Pretty much as Joe said. In fact, exactly as Joe said. Two nails nailed in at B and P as he drew it. Rest the bottom edge of two straight planks (ply) on the nails, with the bottom edge of one that spans B,A, (times 2+) and the bottom edge of the other that spans P,A, (times 2 +) nail them together above A, stick a pencil in the angle formed by B,A,P, at A and move the two planks thus nailed together left to right (whilst keeping their bottom edges firmly anchored on the nails at B and P,) to describe an arc through B,A,P. Can't do this on the wall for some reason? Lay it out on a plywood template, cut it to shape, and transfer it to the wall/opening. You will, of course, have this cost of time and materials built into your price should you need to follow the latter transference or template method. Sliante.
*Draw the arc or circle with CAD and plot the (small) arc section in question full scale to use as a template - I do this all the time with arcs and ellipses. Recently did an ellipse 24" high and 12 feet long (admittedly, using a rollfeed plotter).
*I've used a length of 1/2" pvc pipe as an edge for laying out a large radius curve. I would suggest that if a wall or ceiling, it would be difficult to see the difference of a few feet when the radius is in the 100's and smoothness of the curve counts.
*Phill,
View Image © 1999-2000"The first step towards vice is to shroud innocent actions in mystery, and whoever likes to conceal something sooner or later has reason to conceal it." Aristotle
*I've seen some big architectural millwork jobs with curved and radius walls profiled that were all developed from the cad file....data goes to a CNC machine to cut out templates for the carpenters to build the walls right on top of. The millworkers, cabinetmakers, and anyone else involved use the same file to develop their stuff, knowing it's all going to fit to a tee. Easy to make a full size template of the area you need, as Jeff says.I know the guy in the field is still going to have to know how to do it without benefit of the technology often, but it's amazing what's being done today.
*The radius comes into play by the fact that the great the radius, the flater the arc, and therefore the precision required for the angle layout becomes more critical. I said it would work, I just ventured the opinion that the degree of difficulty was high. If you'll note, someone else described the same procedure I layed out (except they had the architect give them the plot numbers), and found that method fairly easy as all you have to cut is a 90' angle.
*i If you look at the graphic this could be the angle formed at BAP.The angle formed at BAP is the same as the angle formed at BIFF, BAM, KAZOWIE and CRUNCH. This angle is always found at an acute trajectory, trailing from Batman's fist...
*Phill,
View Image © 1999-2000"The first step towards vice is to shroud innocent actions in mystery, and whoever likes to conceal something sooner or later has reason to conceal it." Aristotle
*we alway laid out these arcs from a few known points.. and then lofted them with battens just as you would a boat...to fair the curves....another good source of the math magic are railroad engineers... the arcs and tangents they work with have given them methods they've been using since modern engineering developed about the turn of the century..
*Joe,Your formulas are correct, but because you include "H" in the formula to determine the "ANGLE", it follows that the angle IS a function of the radius, as well as a function of the length of the chord, since "H" is a function of the radius and the length of the chord.In other words, if the length of the chord is held constant, but you allow the radius of the circle to vary, then H will vary also, since "H" is dependent on both measurements, or, is a function of both.To put it in another way, if you were to draw a chord 10 feet long in a circle whose radius were 100 feet, and also draw a chord 10 feet long in a circle whose radius were 200 feet, "H" would be different, since the radius is part of its determination.
*Mr Drake,
View Image © 1999-2000"The first step towards vice is to shroud innocent actions in mystery, and whoever likes to conceal something sooner or later has reason to conceal it." Aristotle
*If you have a compass, and know how to bisect a line, this is easy.To refresh your memories, to bisect any line, set the compass for a length greater than half the length of the line. Set the point at one end of the line, and swing an arc above and below the line, being sure the arcs are long enough to pass the midpoint of the line. Then without changing your compass length, set the point on the other end of the line, and do the same thing. The pairs of arcs will intersect above and below the line. Use a straightedge and connect the intersections of the arcs -- the line so drawn will be perpendicular to the original line, and pass through its center.A line which so "bisects" a chord (of an arc) will pass through the center of the arc. So draw any two chords on the arc for which you are trying to find the center. Bisect them as described above. The two radial lines which bisect the chords you drew, will intersect at the exact center of the arc. The longer the chords the better. It's OK if the chords actually intersect each other. This all assumes you are working with a circular arc (i.e., only one center).In the field, just draw a chord, find the center with a tape measure, draw a perpendicular line with your square. Do it again. The intersection of the two lines is the center.[Sorry, this probably doesn't answer the original question, but could still be useful.]
*Joe,We're really saying the same thing.You're looking at the problem as it pertains to one given circle, with a constant radius. In this case, it would be correct to say that the angle is a function of the length of the chord, as you put it.I was looking at the general case, which would apply to all circles and all chords of those circles, in which case, you would need to know BOTH the radius and the length of the chord to determine the angle.Looking at the problem from this direction, the angle would be a function of both the radius and the length of the chord.
*Mr Drake,
View Image © 1999-2000"The first step towards vice is to shroud innocent actions in mystery, and whoever likes to conceal something sooner or later has reason to conceal it." Aristotle
*Joe,It's just the English language that we're talking about at this point. I'm sure we both understand the mathematics, as well as the dependence of the angle on the radius and the chord length. A more important issue in my mind would be, has any of this information really helped Chris Barry. Given the large radii he works with ( hundreds of feet, as he mentions ) how practical would it be for him to make such a "jig" to scribe the portion of the circle that he needs?Even if he is talking about a small arc of a a circle with a 200 foot radius, ( say 1/6th of the circle ), can you imagine yourself making the plywood jig that he would need to use this method, even if it were on the floor, and not the ceiling?
*I worked out the calculations for an arc, and they are really "interesting" and long. If you really want them, I can post them (after I thoroughly check them again).Your best bet is a CAD program. Draw the circle and cut it with the straight line. Then draw perpendicular lines every so often from the chord to the arc, and measure them. Print out the thing.Go to the site. Lay out your straight chord. Then measure along it, and lay out your perpendicular distances according to your drawings. Connect the dots.Blending the dots into a smooth curve "is an exercise for the student" as a very nasty teacher used to say.
*John,All of the suggestions that have been put forth here have some validity.I still wonder, as I expressed to Joe Fusco in one of my previous posts in this thread, if any of these methods really are helpful to someone working with such large radii ( several hundred feet ) as Chris Barry does.How many "dots" do you need to connect to accurately draw an arc of a circle, that is perhaps 200-500 feet long?I understand the math, and the CAD that it would take to produce the perpendicular lengths, but is it practical, on such a large scale?
*Ken....Easy way to do hundred foot radius arcs...Draw it to a scale that fits your gragh paper and just scale it back up....It's as easy as the ball of string roofing ideas and more necessary.near my ball of string,ajThis is a serious post....Scaling is by far the quickest and easiest method.Ken....What do framers make in your neck of the woods?....Weather here is your worst nightmare...Freezing rain....ice...slop...
*AJ,Strangely enough, we've had an ice storm here in San Antonio, Texas, this past week ( unusual, to say the least ). Put everybody out of work.I won't go into salaries in this thread. I'll discuss it in e-mail if you'd like.As far as scaling goes, you still have to connect the dots. How many of these dots to you need to draw such a huge arc, several hundred feet, perhaps?
*Ken...I think you are missing the point on the arc....The radius is given for a reference but the arc may be only ten feet long....Then all you do is set some nails as Mike said and batten strip past the nails so as to make your own french curving....The huge house I sided last year had arches in the entry porch that were called out in such a way.near the stream...aj
*AJ,Yes, but it also could be the stage in an auditorium, or performining stage, spaning several hundred feet.If so, how would you deal with that?
*Ken....I would think a sheet of reference numbers or and just do the same thing....I think we need an old Greek engineer...near the stream,aj
*
I frequently need to find an arc of a circle when laying out walls or ceiling details. The plans will specify a radius going into the hundreds of feet but I might only need a small portion of the complete circle for my layout.Without using a centerpoint and long tape measure to physically layouton the floor;most times this is impractical because of obstructions; is it possible to find the arc given the length of the radius?