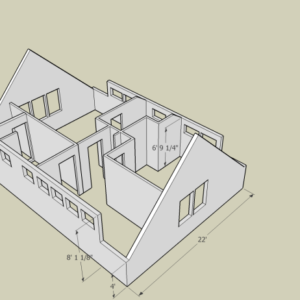
Take a look here, and get out your CMs, or your CM Pros, or even your CM Pro Trigs. Or anything that works.
Shown are the upper walls of a little 2-story place, with a principal pitch of 12:12 bearing on the 4′-0″ kneewalls. All rafters are 2x12s.
A shed dormer runs across much of the front and back, each with a different pitch. Front and back wall heights at the shed rafter seats are shown.
The ridge won’t be structural, as we will do collar ties as ceiling joists. To get toenail purchase along most of the rafter plumb cuts, we might use an LVL at 16 or 18 deep. But that’s overkill, right? How about just a 2×12 with a 2×6 under it? But, ridge doesn’t come into play for this question.
Calculate for me the pitches of the shed roof rafters, but please, show me the development of the math. Thanks.
I can work it out graphically with CAD, to get real close, and I get 7.578:12 for the front and 9.016:12 for the rear, but I am wanting to see how math is used to get them exactly.
Edited 1/11/2007 11:28 am ET by Gene_Davis




















Replies
Gene, need the height from floor to top of ridge or from top of wall to top of ridge. Otherwise, if your not doing a structural ridge, why not use 1x12 roughsawn for the ridge, then just be sure to align rafters, a lot easier to work with than 2x12's or LVL's. Anyway 7.578 and 9.016 , looks to me to be close enough to 7 1/2 /12 and 9/12 respectively to start cutting rafters.
Geoff
RUN would equal 22 divided by 2 = 11' minus 1/2 ridge = 10'-11-1/4 "
RISE A = 10'-11-1/4" + 4' minus 8'-1-1/8" = 6'-10-1/8"
RISE B = 10'-11-1/4" + 4' minus 6'-9-1/4" = 8'-2"
construction master makes life easy from here, plug in rise and run and calc. pitch and diag.
A- diag. 12-10-53/64" pitch 7-33/64" 7.515625
B- diag. 13' 7-51/64" pitch 8-61/64" 8.953125
Without CM, AxA + BxB = CxC to calculate diagonal, then sine cosine or tangent to calc angles.
Edited 1/11/2007 1:02 pm ET by Muttly
Thus far I have gotten three replies all done using calculators. One came here, and two came in response to the same Q over at another forum.I used my CAD program to plug all into the 2D model I built, and as can be seen in the attached zoom-in up at the ridge, none are exactly right. I did not show my graphical solution pitches of 9.016 (front) and 7.578 (rear), which by the way came closer to having the tops all meet at the peak.I am wondering what the math is to get it right, exactly.
The peaks are set in the same plane, it's the heel end that will move, I calculated 0" of heel height, it will be close enough to cut the ridge angle, if you want to be precise, take my previous #'s and subtract the desired heel height at outside wall from the rise #.
You will also need to draw in the 1-1/2" ridge beam in your drawing.
If we use 4" for a heel height:
RISE A = 10'-11-1/4" + 4' minus 8'-1-1/8" = 6'-10-1/8" - 4" heel = 6'-6-1/8"
RISE B = 10'-11-1/4" + 4' minus 6'-9-1/4" = 8'-2" - 4" heel = 7'-10"
A- diag. 12'-8-47/64" pitch 7-9/64" 7.140625
B- diag. 13' -5-7/16" pitch 8-19/32" 8.59375
Gene: 7.56112/12 and 9.00283/12
Right or wrong, I posted the same results based on the latest info at the JLC Forum. Sorry I haven't really answered your question yet and given a blow by blow analysis of the math ... I'm having a bad day.
Check out Joe Carola's drawings (scroll down below the "Fixed Ridge Calculator"). Even if my figures are wrong I think he's got the correct procedure.Joe Bartok
It would be helpful to know what the thickness of the ext. wall is , as well as if you are planing the rafters to the inside corner of the walls top plate. (I assume you are.)
They are 2x6, and the heel of the cuts match the inside wall line.
Let's get everyone on the same problem, with all the information.
The missing piece is the ridge thickness. Let's say it is a 2x, thus 1.5" in thickness, and all rafters must have their tops plane to the ridge.
7-9/16 and 9 are real close, but I don't think they are exact, because my CAD package, which works to 6 decimal inches of precision, doesn't have the lines planing.
Edited 1/11/2007 2:20 pm ET by Gene_Davis
Gene,The front shed roof, the pitch angle I get is 32.22° or 7.562655/12 or 7-9/16 pitch.The back shed roof, the pitch angle I get is 36.87° or 9.000034/12 or 9” pitch.Sorry Gene, but I 'll show the math when I get back from taking my son to wrestling practice.Joe Carola
Edited 1/11/2007 5:22 pm ET by Framer
I was just headed out the door when I realised that the answer I had posted here was in error. Because of the differant pitches one has to add the height of the 12/12 plumb cut HAP to the originial rise and work the problem from there . My original solution would have the bottoms of the rafters planing but not the tops.Edited 1/11/2007 3:00 pm ET by dovetail97128
Edited 1/11/2007 4:17 pm ET by dovetail97128
I might use the 2 x 12 ridge, but put it at the bottom and a 2 x 4 at the top. Your diagonal cut for the ridge is only 16 1/4". Hold the 2 x 12 up so that the drywall planes to true center at the ridge line.
Ok,. I will try this again after taking the different pitches into account.
First I had to revisit the rule of using the "true rafter line" line (drawn from apex of birdsmouth parallel to the rafter until it intersects the ridge
I also needed to calculate the HAP on the 12/12 pitch roof. I did this assuming a 6" seat so the bottom of rafter planed to top inside of frame wall. Using a 11 1/2 wide rafter I get a HAP of 9 13/16" (6' run, 11 1/2" diag.), Hit rise on CM
Now I added the HAP 9 13/16" to my 11' rise(rise at 11' run on a 12/12)and that =11' 9 13/16 .
That is the height to the top of ridge center off the floor 12/12 pitch
Now I work backwards...
For the one side of the building ("A") I subtract the 4' 1 1/8" difference in wall height plus the 9 13/16" HAP.
11' 9 13/16"- (4' 1 1/8" + 9 13/16")= 6' 10 7/8 rise, over the 11' run
Side "B"
11' 913/16"-( 2'91/4" + 9 13/16")= 8'2 3/4" rise over the 11' run.
So I end up with
Side "A" = 7 9/16" pitch , 32.12 deg, or 7.534091"
Side "B" = 9" pitch , 36.80 deg , or 8.977273"
been wrong with this stuff too many times in my life so if I am here it is just one more time .
and I really need to find a job ! lol
Oh Yeah and you cannot get the shed roofs rafter bottoms to plane into the inside upper corner of the wall . You would need to adjust wall heights to do that.
That should read that "I" cannot figure out how to keep the shed roofs bottom rafter plane intersecting with the inside upper plate line. I am sure someone can . Be happy to learn though.
Edited 1/11/2007 7:06 pm ET by dovetail97128
Gene: Run = 10' - 5 3/4"
Rises: 9' - 0 13/32" and 7' - 8 17/32"
This is going not to a theoretical ridge line but to the face of the ridge board.
I'll be back tomorrow but I'm sure Joe C. will have the detailed answer you are after posted later tonite. :)Joe Bartok
Thanks to all who provided their solutions. I'm not going to grade papers, but I'll say this, after sitting down with a pencil and a piece of paper.A lot of you gave wrong answers. This is a pretty basic roof geometry problem, and if I were to use this problem in a hiring test for framing gang foremen, you would not be hired.It doesn't have to do with circle tangents.It is all about solutions to right triangles, as is most of all roof geometry.Thanks to Joe Bartok, who rolled the math into his online roof calculator, which provides the right answers. Framer, you got it right too, but didn't show me your workout. If any of you that attempted it want to try again, you might try to do it the way I went, and first get the distance from the floor to the top of the ridge 2x.Hint : to the nearest 32nd, it is 15'-9 21/32"
This was also posted in the JLC Forum:
Actually we owe Joe Carola a thank you. He originally solved this problem and posted the geometry and trig in the following forums:JLC Forum Fixed Ridge Height ThreadJoseph Fusco Forum Fixed Ridge Height ThreadThe web calculator is based on his math and the original drawings are on the web page below the calculator.I tackled this again last night, this time using decimal inches and angles rounded to five decimal places.Pitch Angle = 32.22660°, Slope = 7.56459/12Pitch Angle = 36.88846°, Slope = 9.00608/12I'm not posting the details yet because I used two methods to solve for the plumb cuts and they disagree at the 1/100ths of an inch. To be sure, this is rough framing and nothing to worry about if cutting a rafter. But there shouldn't be this discrepancy employing trigonometry.Ha! Ha! I can't even agree with myself! :)EDIT: Gene, the "spring point" measured from the floor in inches is:11 × 12 – 5.5 – .75 + 48 + 11.25/cos 45°= 189.65990 = 15' – 9 21/32"I used the same point but subtracted the 48" from all dimensions.Joe Bartok
In case anyone is interested (or, like myself, is totally anal and has a habit of absolutely beating the math to death in nit-picking detail), check out the JLC Forum thread: "The math, please"
Two other resolutions have been posted:
Ed Michnik ... this one is the easiest to follow.
Timbersmith ... the formula for the "circle tangent" solution is at the bottom of this Mathworld page.
Cool! Now we have three ways of figuring these rafters. :)
Joe Bartok
Edited 1/12/2007 3:04 pm ET by JoeBartok
How do you come up with 15' 9 21/32" as the top of ridge height?
The dimensions you give are clear, 12/12 pitch w/ 22' span: rise equals 132" or 11' ....add 48" height of lower wall , total rise equals 180" or 15' .....please enlighten me, in fact this is exactly what I first posted was the info needed to solve your question.
I believe I calced. the correct pitch of the roof sections in question, do I get the job?
Geoff
>> The dimensions you give are clear, 12/12 pitch w/ 22' span: rise equals 132" or 11' ....add 48" height of lower wall , total rise equals 180" or 15' .....please enlighten me, in fact this is exactly what I first posted was the info needed to solve your question. <<Geoffrey,Your not figuring the H.A.P cut for the thickness of the 11-1/4" 2x12.I figure from the inside of the wall and just add the height of the plumbcut for the 11-1/4" 2x12. I divide the span in half deducting the thickness of the ridge first and then suntract the 5.5" width of the wall.22’-1-1/2" = 21'10-1/2"/2 = 10’ 11-1/4” – 5.5” = 10’ 5-3/4” 10’ 5-3/4” = (Run and Rise from inside of plate to bottom of rafter)12 [Inch [Pitch]11.25 [Inch] [Run][Diag] = 15.9099” (Height of 12/12 common plumbcut at ridge)[+] 10’ 5-3/4” = 11’ 9-21/32” (Total Rise from 4’ kneewall to Top of ridge)+ 4’ = 15’9-21/32” (Total Rise from deck to top of Ridge)If you want the total rise from the outside of the plate using the H.A.P. cut.15.9099"-5.5" =10.4099 + 10'11-1/4" = 11' 9-21/32" + 4' = 15' 9-21/32"
Joe Carola
Joe, thanks for the response,I understand the calcs involved but what I understood Gene to be asking was a straight forward description of figuring the pitch, I used the therorectical lines to get a very close, but not "dead on" calculation, simply the Pythagorean theorem, A squared plus B squared = C squared. I think Gene suckered every one in as if he was looking for some simple info, then when differing answers( 1/100th of an inch?) appeared he suddenly swoops in and discounts everyone's answers (the I wouldn't hire response) and acts like we're a bunch of numb nuts who can't add. As he himself said " it's simple trig." well, then don't go scoffing at people who give a simple answer. If he wanted an in depth discussion of the calcs to 6 decimal places he should have said so upfront!
I'm done venting.
Gene, thanks for the diagram
Geoff
Geoff, your nuts probably aren't numb and of course, you can add. Furthermore, your first response, way back at the beginning of the thread, was certainly OK for cutting rafters.
No problem with that.
But for the unschooled or beginners amongst us, I was looking for the workout, the way you got from point A to B. The route to the answers.
Long ago when I was in school the instructors would fail our test answers unless we showed our workouts. Answers were not sufficient, as they could have been copied.
I looked back at my first post, and it seems as if I actually gave all the pertinent information except for the actual depth of a 2x12. I thought everyone got them at a depth of 11 1/4", but apparently some of us out there live in the land of big wood, and they in fact come deeper.
I didn't think I was drawing others into a seemingly simple problem, and then shorting them with the facts needed to figure. I was just trying one on all you pros who are used to getting one solved with three punches on your CM Pros. As for my CAD pic, I inadvertently set the results accuracy at something like six decimal inches. Sorry. My skilsaw only cuts to four.
Long ago when I was in school the instructors would fail our test answers unless we showed our workouts.
Out here, in carpenterland, we don't have to show our workouts. We have the house as proof that we know what we are doing.
I'm lucky I don't have to vent. I'm smart enought NOT to read the problem LOL!
blue"...if you just do what you think is best testing those limits... it's pretty easy to find exactly where the line is...."
From the best of TauntonU.
Gene
When I was in college I would have recieved partial credit for giving an answer like yours! Thats not the exact answer.
You cant have an exact answer when you round no.s off. Calculators round no.s!
Just trying to be nit-picky!
So as I score it you and Geoffry would recieve about the same credit! :)
Doug
Here's a pic with some of the numbers. Sorry if I was not clear before.
A lot of you gave wrong answers. This is a pretty basic roof geometry problem, and if I were to use this problem in a hiring test for framing gang foremen, you would not be hired.
I just found this thread 15 minutes ago. After reading all the posts fairly quickly, I've got to say that most here probably wouldn't want to work for you. I'd have a hard time carrying a laptop in my nail bags while rolling trusses
hehehehehehe
You wouldn't get hired, Tim. We consider bigfoots and chainsaws too dangerous. Axex and hatchets, maybe. But them big whirlers are just plain scary.
But we could sub out our roof cut calcs to you. Howzzat?
The problem I posted is a common everyday one for folks doing remodeling, when a shed boost is done to a roof to gain new floor space. Fix the wall height so precut studs are used, hang new rafters off the fixed ridge wherever it is, let the pitch fall where it may, and you gotta figure. Any pocket calc that does square roots will do, but your CM Pro will work just fine.
View Image
I was just bustin' your chops.
Picture looks good. What is it about framing pictures that is so cool? :-)
would be very interesting to see someone try to figure out all those #'s behind the
decimal point on a framing square!! i'd have framed it while you guys were still arguing it!!!
I don't know about all the others, Mike, but I'm on the edge of my seat.
Got a digital camera? Show us the work-out, all done with a framing square. I'm sure you can do it.
Here ya go. Let's start over with some fresh numbers.
Horizontal distance from face of ridge to inside of wall is 10'-5 3/4"
Let's say the rise from your wall plate to the top of the ridge is 6'-9"
You're gonna use a 2x12 (11 1/4") and cut a full seat (6") for the 2x6 wall plus 1/2" ply sheathing you put on it.
What's yer pitch and rafter length?
When you're snapping those pics, put a stopwatch in 'em so we can tell how long it's taking you.
Gene,
I have taken part in this thread and enjoyed it. But if this was just a simple common rafter being cut to the dimension you just challenged with I could do it quite rapidly using the 1/12 scale on my faming sq..
None of your numbers are difficult to scale off using the sq. and while I doubt I would be accurate to the 3rd. decimal point I would have no doubt I would be accurate enough to frame with.
The old boys did it all the time and were really good at it.
Not as fast perhaps as the modern calculator but not far behind it either. Since I don't carry a computer around with me the "original rafter computer" (Framing Square)would get the job done just fine. Plus using it helps me envision the problem.
Gene
isn't the full seat cut 6" INCLUDING 1/2 " sheathing on a 2x6 wall ?
>> Oh Yeah and you cannot get the shed roofs rafter bottoms to plane into the inside upper corner of the wall . You would need to adjust wall heights to do that.
That should read that "I" cannot figure out how to keep the shed roofs bottom rafter plane intersecting with the inside upper plate line. I am sure someone can . Be happy to learn though.<<Yes you can, I always do and go to the inside of the plate when you have a fixed wall height and fixed ridge height. The size of the rafter will always change the pitch also. Gene's using 2x12's on both rafters for this roof. If he changed the shed rafters to a 2x8, the pitch would chnage.Look at this thread I started a while back.http://forums.jlconline.com/forums/showthread.php?t=28296&highlight=fixed+ridge+heightJoe Carola
Joe,
I actually went back later that day when I had time and did work out the problem so that the rafter bottom planed. I just didn't come back here and post that . My original solution would have had a 6 5/16" seat on the one shed, close but not perfect. Gene had kindly forwarded me you posts at JLC's forum (I hadn't been there before) so I have read them and appreciate your posting them.
Over all I came within hundredths of in. of your guys solution while using different ridge hgt.(11 1/2") and wall thickness (6"). ""So I end up with
Side "A" = 7 9/16" pitch , 32.12 deg, or 7.534091"
Side "B" = 9" pitch , 36.80 deg , or 8.977273"" I figure I could have talked Gene into at least letting me pack lumber on his site. ;-) I like the method of solving it using the actual lumber and the speed sq.. Cute trick.
In the past if I doubted the outcome of my math would I lay the problem all out to scale using a framing sq. simply helps me see the issues. ( I much prefer framing sq.'s to speed sq.'s for this work)
Thanks for your postings.
Might as well post some more goodies in this forum.
First, I made a grave error in the trig version of the "math workout" over at JLC.
Angle at rafter foot = arctan(11.25/156.12742) = 4.12141°
The equation above should read:
Angle at rafter foot = arcsin(11.25/156.12742) = 4.13212°
Check out the drawings in the link by Joe Carola a.k.a. "Framer". The dimensions in question are clearly a rise/diagonal, or the sine of the angle. Hence, we use arcsin, not arctan, to find the angle.
A corrected version of the cyphering is attached.
The next link is based on the "circle tangent" solution by "Timbersmith":
Tangent to Circle: Solution of Fixed Height Ridge
I've shown the algebra used to solve for the rafter pitch angle ... maybe the math is right this time. ;)
Joe Bartok
Edited 1/13/2007 11:54 am ET by JoeBartok
>> I like the method of solving it using the actual lumber and the speed sq.. Cute trick.
In the past if I doubted the outcome of my math would I lay the problem all out to scale using a framing sq. simply helps me see the issues.<<I do a lot of additions and I deal with a lot of situations where the top of the addition ridge running perpendicular to the existing ridge has to match the existing ridge height. I also do many shed dormer additions where the top of the shed rafters has to match the top of the existing ridge.With a shed dormer and this thread figuring out the math for me is something I like to know. When it comes right down to it, once you have your set wall height, you don't need any math at all, you just stick a rafter up planning the top edge and scribing a plumbcut and holding the bottom of the rafter flush to the inside of the top plate and you're done.If you want to do the math and not even waste time scribing, all you need to do is measure from the top of the existing ridge and to the inside of the top plate and that's your diagonal measurement. Now you have that and your run from the inside of the plate to the face of the ridge.You punch the diagonal measurement as diagonal and the run as run and hit pitch. Snap the diagonal measurement on the rafter and slide the speedsquare until you hit the pitch angle that was given on the chalkline and then look at what the angle says at the top of the rafter and that's the real pitch.This is ten times faster than bringing up a rafter and scribing it. Or you can measure from the top plate to the top of the ridge and get the rise and use the run to get the diagonal, either way. Measuring the diagonal from the top of the ridge to the inside of the plate is most accurate, especially for additions because most of the time the existing ridge isn't straight and you have to either straighten it or cut each rafter a little different.When I have a reversed gable roof to cut in and match an existing ridge, I just measure the height from the top of the existing plate to the existing ridge and do the math like I've described and it works every time without even going up to the deck. I have the rafters cut before the addition walls are even up.Like I've also said before it doesn't matter whether I use a 2x6 rafter or a 1-3/4" x 14" microlam, going to the inside of the top plate will always work out perfect. The only difference is that the bigger the rafter the lower the pitch is.Now if you’re trying to match existing fascia heights, that's easy also. If they want the overhang length to match, then you have to adjust plate heights because most of the time the existing rafters are smaller than the addition rafters. Joe Carola
Joe,
The first home I ever contracted was an octagon that was longer than it was wide. This was back around 1972-3 or so. It had 4 x 12 hip beams and 2 x 12 commons.
Being a mathmaticly challanged individual I measured all the common rafters for the job exactly the way you describe.