Closed-Cell Foam between Studs Is a Waste
What really matters is the R-value of the whole wall, not just that of the insulation.
Open-cell spray foam has an R-value of about R-3.7 per inch, while closed-cell spray foam has an R-value that may be as high as R-6.5 per inch. If you want to install spray foam in a stud wall, and price is no object, then it would seem to make sense to specify closed-cell spray foam, right? Well, not necessarily. Both walls are affected by thermal bridging — the loss of heat through the wood framing — but there’s more to it than that.
What really matters is the R-value of the whole wall, not just that of the insulation. There isn’t much difference in the whole-wall R-value between a wall insulated with open-cell spray foam and one insulated with closed-cell spray foam.
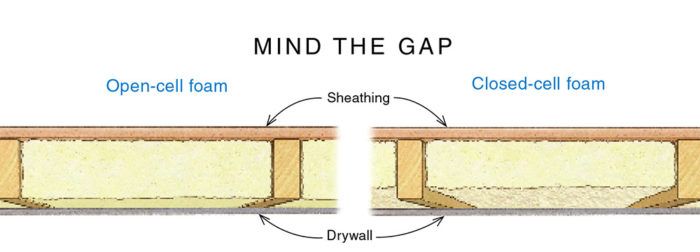
 To understand why, we need to start by understanding the “trimmability” of cured foam. Closed-cell foam is so dense that it is difficult to trim. To avoid having to trim closed-cell foam in a 2×4 wall, the installer will usually stop at a maximum depth of about 3 in., instead of the full 3-1⁄2 in. depth of the stud cavity. This leaves the typically bumpy surface of cured foam and about a 1⁄2-in. gap to the back of the drywall. Open-cell spray foam isn’t as dense, so it’s easy to trim. Installers of open-cell spray foam will fill a 3-1⁄2-in.-deep cavity completely, allowing the foam to expand until it is proud of the studs. Once cured, the soft foam is easily trimmed flush with the studs.
To understand why, we need to start by understanding the “trimmability” of cured foam. Closed-cell foam is so dense that it is difficult to trim. To avoid having to trim closed-cell foam in a 2×4 wall, the installer will usually stop at a maximum depth of about 3 in., instead of the full 3-1⁄2 in. depth of the stud cavity. This leaves the typically bumpy surface of cured foam and about a 1⁄2-in. gap to the back of the drywall. Open-cell spray foam isn’t as dense, so it’s easy to trim. Installers of open-cell spray foam will fill a 3-1⁄2-in.-deep cavity completely, allowing the foam to expand until it is proud of the studs. Once cured, the soft foam is easily trimmed flush with the studs.
Whole-wall R-values
To calculate the whole-wall R-value of a wall, we have to divide it into areas, each with distinct R-values. For example, a 2×4 wall without any windows can be divided into two areas: insulated stud bays and wood framing. A typical wood-framed wall has a “framing factor” of 25%. That means that about 25% of the wall area consists of studs, plates, and headers. The remaining 75% of the wall consists of either stud bays filled with insulation or openings for windows or doors.
To calculate whole-wall R-value, you first need to calculate the whole-wall U-factor. (U-factor is the reciprocal of R-value: U=1/R.) Let’s call the U-factor of the insulation “UI,” and the U-factor of the framing “UF.” Here’s how we calculate whole-wall U-factor for a wall without any windows or doors:
Whole-wall U-factor =
(UI x % area devoted to insulation) +
(UF x % area devoted to framing)
When stud bays are partially filled with closed-cell spray foam, the exposed portion of the studs reduces their R-value in comparison to a wall that is totally filled with open-cell spray foam. For example, if a 2×4 wall has 3 in. of closed-cell foam insulation, the R-value of the studs is based on a stud depth of 3 in., not 3-1⁄2 in. (because the exposed portions of the studs are basically “indoors” and not part of the insulated wall assembly). As a result, the heat loss due to thermal bridging through the framing is greater in a wall with closed-cell foam than it would be in a wall with open-cell foam.
Consequently, if you install a closed-cell foam insulation with a high R-value per inch between your studs, you don’t really get the full value of your investment. Closed-cell spray foam is expensive, and the incremental cost is mostly money down the drain. There are more cost-effective energy upgrades, such as exterior rigid foam or mineral-wool insulation, as I point out below. It’s also worth considering an even more important issue: Most brands of closed-cell spray foam are more injurious to the atmosphere than open-cell spray foams, since most closed-cell spray foam is manufactured with a blowing agent that has a high global-warming potential.
The examples aren’t perfect
I’m aware that the whole-wall R-value calculations in the table are simplified versions of actual whole-wall R-value calculations. I haven’t included the R-value of the exterior OSB sheathing, the interior drywall, or the associated air films. Moreover, the table doesn’t reflect the entire range of framing factors of different buildings.
That said, the table is useful. It demonstrates the calculation method and does a good job of estimating the incremental R-value attributable to an upgrade from open-cell to closed-cell foam. While it’s true that actual whole-wall R-values will usually be higher than the values shown in the table (due to the R-values of the sheathing, drywall, and air-barrier membranes), both types of wall (open-cell and closed-cell) benefit equally from these additional R-values.
While I’ve focused on walls, the same analysis applies to cathedral ceiling assemblies. If rafter bays are completely filled with fluffy insulation (except for a ventilation channel directly below the sheathing), thermal bridging through the rafters will be less significant than when 4 in. of each rafter protrudes inward beyond the depth of a skimpy application of spray foam.
So what’s the solution?
At this point, we need to consider the use of exterior rigid foam. The calculations for adding thicker continuous insulation on the exterior side of the wall sheathing are much more favorable to incremental investments than the calculations for insulation installed between studs.
If you install a high R-value continuous rigid insulation on the exterior side of the sheathing—for example, rigid foam or mineral wool—all of the insulation’s R-value contributes to the whole-wall R-value (except, of course, for areas taken up by windows and doors). (One word of caution: it’s important to calculate the thickness of exterior insulation correctly so that moisture doesn’t accumulate on the interior face of the sheathing in cold weather.)
Unlike between-studs insulation, exterior high R-value insulation helps to minimize the thermal bridging effect of the studs. Used properly, it also reduces the need for a vapor retarder by keeping the sheathing warmer than the dew point. Even though exterior rigid insulation requires extra detailing around windows and doors, it still offers excellent value for your money.
RELATED STORIES
- Crash Course in Control Layers
- An Easy Way to Build a Well-Insulated House
- Dense-Pack Cellulose Insulation Done Right
For more photos, drawings, and details, click the View PDF button below:
Fine Homebuilding Recommended Products Fine Homebuilding receives a commission for items purchased through links on this site, including Amazon Associates and other affiliate advertising programs. Utility Knife Respirator Mask Caulking Gun





View Comments
What about the air seal factor? Vapor barrier after 2"?
This makes no sense. I agree that there should be a continuous insulation but your comments are simply not true and give foam a bad name.
Can someone answer for me a much more basic question? What's the R-value of a wall that is 50% R10 and 50% R20?
13.333?
Yes, that's what I calculated with the formula. Can someone explain why it's not 15? Thanks.
Chris1271: Its 13.333 because of what is called the 'Law of Diminishing Returns'. The whole wall works to reduce loss to R10. Yet, there is some loss and now only the remaining heat is left. The remaining walls either don't stop any loss R0 or stop R10 of this lesser remaining heat. So the second R10 does not have as much heat to hold back as the original R10 does. Its better understood when using the U-factors because that is a measure of heat's pressure through the wall. To top it all off, the other law of thermal dynamics is that heat tends toward 'cold' e.g. the lack of heat, so the second R10 serves a dam that redirects the heat flow toward the colder R0.
A corollary of this is found in statistics as seen in Let's Make A Deal. Choose a door. They reveal another door isn't the good prize. Your chances of having the winning door if you keep your first choice may seem like 50% but statistics show that it is only 33%. I bet you can google this as it is a basic example in most business statistic courses.
Thanks, ktkcad, but I still don't get it. Anyone else want to give it a try?
The only analogy I can think of is an old math problem: If you drive 10 mph for 10 miles and then drive 20 mph for another 10 miles, what's your average speed? 13.3333 mph, yes, I know and I know why it's the answer. But is this analogy even relevant to the R-Value problem? How?
I'm not trying to turn this into a "Cartalk" puzzler, really I'm not. I guess I just don't understand the nature of what it means when we say "R-Value."
Chris1271,
I did some research and found this article particularly helpful:
http://www.greenbuildingadvisor.com/articles/dept/building-science/fundamentals-series-and-parallel-heat-flow
To answer your question again... suppose you had a wall that consisted of a 2" inner layer of [new]XPS foam and an outer layer of 5" of Type II EPS foam. The inner layer would be R-10 and the outer layer would be R20 (assuming its about 65 degrees...). I 'think' this wall would have an average R value of R15.
Things change though when we introduce studs! Because a stud extends from outside to inside, warm indoor air now has a choice how to get outside to the colder air. It can travel through the insulation or it can travel through the stud. The XPS/EPS wall above doesn't encounter this problem because the indoor heat encounters only one layer at a time any where on the interior side of the wall.
This is why you have to convert the R Value to the U factor. R values deal with uniform, singular layers. It was designed to provide ratings for insulation materials to keep insulation companies honest. U factor is more helpful as it deals with whole wall assemblies where thermal bridging and multi-dimensional heat flow may exist. Part of this may be because U factor deals with more than just conductivity like R value. It takes into consideration radiation and convection as well (I think). This is why windows use U-factors rather than R value as they are complex enclosures all within themselves.
You can see why a lot of people want the R value metric to go away altogether as it isn't too helpful in measuring heat flow through an entire assembly.
Check out the article I posted. So much wisdom at Greenbuildingadvisor.com
Chris, here is an excerpt from another great article from Allison Bailes III.
"Now, we can't just average the R-values. If we did that here, we'd get R-30, and we'd be wrong. ***Heat will take the path of least resistance, and the less resistance you give it, the more heat will flow***. If you've studied physics, engineering, or building science, you've probably seen the equation for heat flow by conduction: Q = UA ΔT = 1/R ∙ A ΔT"
Read more: http://www.greenbuildingadvisor.com/blogs/dept/building-science/there-downside-lumpy-attic-insulation#ixzz4n3BpLIjx
Follow us: @gbadvisor on Twitter | GreenBuildingAdvisor on Facebook
Thanks, Rick, your explanation and the "flat or lumpy" article you posted were very helpful. I think I get it now. (Thanks, too, Allison).
I suppose It's not about the resistance to heat flow, it's more about the TOTAL heat loss. And, because heat flows via the path of least resistance, the effect of a low r-value section of the wall is disproportionate. I'm still trying to come up with an intuitive analogy. I keep coming back to a bucket with holes in it or a sieve of some sort. In that situation, I think u-factor would be comparable to the gallons per minute of water flow out of the bucket. Maybe. I gotta think it through a bit more.
One minor comment: Take another look at your innerR10/outerR20 scenario. I think the total value of the wall you describe is R30. Certainly it's more than R20...adding R10 on top of an existing R20 wall shouldn't diminish the performance of the wall, it should improve it, right?
Chris, another way to look at this. You're not averaging R-values, you're averaging energy transmission or conductance. R-value is the inverse of conductance or divide 1/conductance to get R-value. Presenting it as R-value is just a fancy way to describe insulation performance to the public that likes insulation values that are higher to mean they're better. Conductance is a measurement of how easily energy is transferred through a material. Copper wire has a very large conductance and insulation has a very low conductance. Compare the numbers on this very handy spreadsheet (http://tinyurl.com/43gd32) Guess what the copper manufactures use to describe the power of their wires? They don't use R-value, they use conductance because the higher the number the better. So, let's take your values and transcribe them into conductance. You have half of your wall conducting at 1/R10 = 0.1 and the other half conducting at 1/R20 = 0.05. Notice the R-20 wall has a lower conductance because energy flows through it slower. Now average those two numbers. (0.1+0.05)/2=? Then convert that back to the fancy public approved R-value and tell me what you get.
At least with the costs in my area, I don't agree with Chris's argument.
Closed cell is about the same $/R (twice the cost but twice the R) so you can use half the amount if you have reached diminishing returns, or more if you want it in for a given size cavity.
However, closed cell 2"+ is a vapor barrier, adds to the structural integrity of the framing, and is supposed to last better (maintain R value) over time.
This guy has absolutely no idea what he is talking about. The "x" factor of this stuff is the air seal quality. That's why foam gets around 50% better energy efficiency on structures across the board.
You can do more with 10 R of closed cell foam than 50 R of fiberglass/cellulose. R value itself is antiquated and only used now to keep fiberglass in the running. It does not take wind into account at all, which is much more important than the ability to transfer heat.
Anything other than foam will help facilitate dust mites, degrade, get into your air supply, and COST you tens of thousands over the lifetime of the building. This is common knowledge.
Stop spouting nonsense. This is an absolutely ludacris article.
Chris1271: This is from Wikipedia's R-Value (insulation) article. The quoted section is from about 3/4 of the way down the article. I replaced the numbers to fit your situation (50%/50% instead of 10%/90% in their example)
"Multiple layers
In calculating the R-value of a multi-layered installation, the R-values of the individual layers are added:[37]
R-value(outside air film) + R-value(brick) + R-value(sheathing) + R-value(insulation) + R-value(plasterboard) + R-value(inside air film) = R-value(total).
To account for other components in a wall such as framing, first calculate the U-value (=1/R-value) of each component, then the area-weighted average U-value. The average R-value will be 1/(this average U-value). For example, if 50% of the area is 2 inches of one kind of insulation (R-value 10) and 50% is 2 inches of another insulation (R-value 20), the area-weighted U-value is 0.5/10 + 0.5/20 = 0.075 and the weighted R-value is 1/0.075 = 13.3333.
“[Deleted]”
Why not both? I'm doing 2" closed cell and then filling the rest of the cavity with open cell. Closed cell adds strength and vapor barrier and not that much more cost since it's only a couple of inches.