Three Ways to Lay Out an Elliptical Curve
Ellipses can provide striking, graceful curves on a building, but they can be tricky to build.

A roof of curves proves the technique: As part of the crew working on the restoration of the Conservatory of Flowers in San Francisco, the author was able to refine his ability to create ellipical rafters.
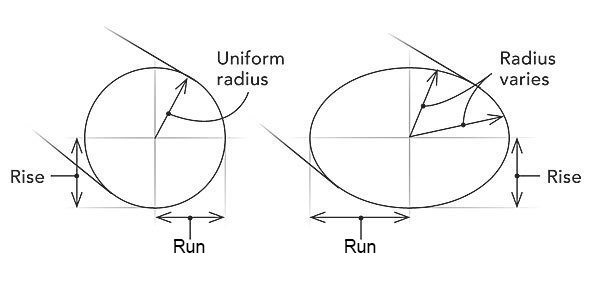
As defined by Merriam-Webster’s Collegiate Dictionary, an ellipse is “a closed plane curve generated by a point moving in such a way that the sums of its distances from two fixed points [foci] is a constant; a plane section of a right circular cone that is a closed curve.” Got it? Luckily, it’s a lot easier to see an ellipse than to understand its definition. Just cut a dowel to 90° at one end and to 45° at the other. The square cut creates a circle with a uniform radius as wide as it is tall. The 45° cut end reveals an ellipse, wider than it is tall.
This ellipse is an example of the geometry of some larger building components. Because these curves are quantifiable, their rise and run can be determined using the conventions of roof framing. For instance, a cove ceiling with a common section that is a simple 12-in. quarter radius would have a corner strut or hip that is a quarter ellipse with a rise of 12 in. and a run of 17 in.
There are several ways to lay out an ellipse. Here, I’ll describe three using that 12:17 rise:run ratio. The first is the string method, which is the most familiar. Use string that won’t stretch, although longer lengths of string tend to stretch, no matter what. The string length can be found by formula, but sometimes it’s simpler just to pull a string around the two foci and to a known point on the curve, such as, in this example, up 12 in. on the minor axis.
The second technique, which is derived straight from the determined rise and run, is to use a trammel. The trammel rides around the square corner of a piece of plywood or other suitable material. The trammel-drawn curve gives the correct ellipse for a regular hip on a 12-in. radial cove ceiling or curved-rafter roof. To draw a hip on an octagonal roof, the trammel is set up with a 12-in. rise and 13-in. run.
The third is an arithmetic plotting, also known as lofting, which can also be applied to any curve. This method comes in handy when you need to derive a hip or valley from an existing, unquantified curve, or if the ellipse is too big to draw with a trammel. During the restoration of San Francisco’s Conservatory of Flowers, both scenarios were true. We drew a grid of 12-in. squares on the floor and then calculated the shape of the curved common rafters, hips, and valleys. Once the hips and valleys were cut to shape, we cut the backing with a changing double bevel that began as two 45° cuts at the bottom plumb end of the curve and diminished to a single flat edge at the top, level end.
What is an ellipse?
The end of a square-cut dowel is a circle, in which the rise (height) and the run (width) are the same, resulting in a uniform radius. But cut the dowel at 45°, and the end is an ellipse, which is wider than it is high. Its radius is variable.
Use a string
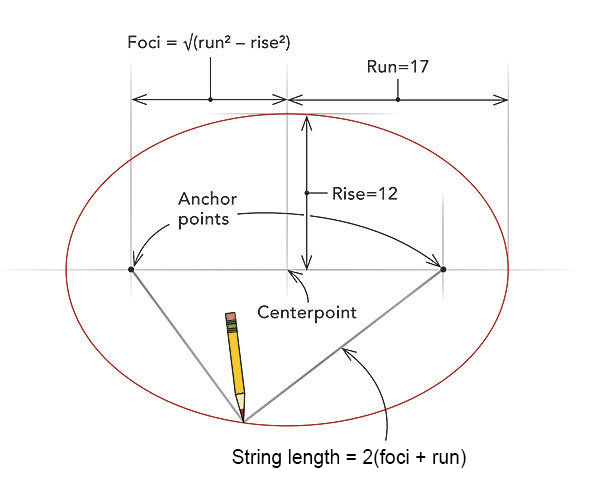
Draw an ellipse with a string, two pins, and a pencil. First, draw a horizontal line and mark a centerpoint. Next, determine the rise and run of the ellipse. The string’s anchor points, called the foci, are located with the following equation: foci= √(run² – rise²). The string length can be calculated this way: string length = 2(foci + run). After finding the centerpoint and foci, attach a nonstretching string of the correct length to nails or screws driven in at the foci. Using the string to restrain the pencil, draw the ellipse.
Use a stick
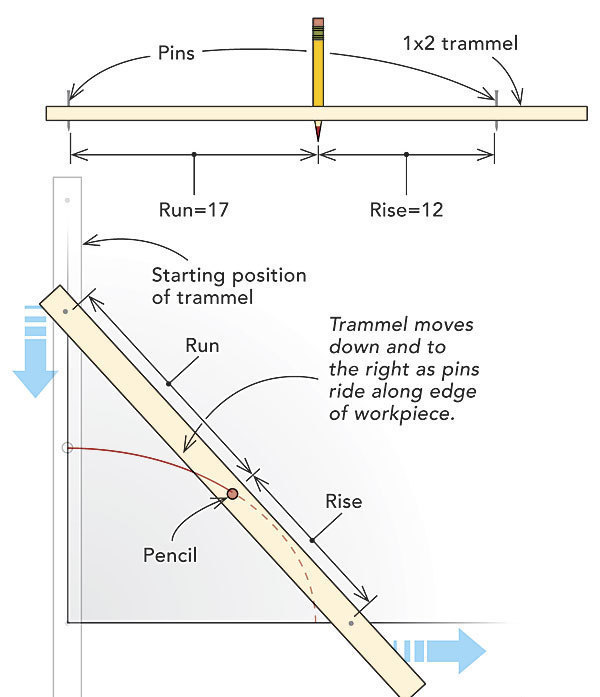
Drill a hole for a pencil in the middle of a 1×2. From the pencil’s centerline, measure the distance of the desired rise (the y coordinate) of the ellipse (for example, 12 in.), and drive a screw or nail through the trammel. In the opposite direction, measure the distance of the run (the x coordinate; 17 in., for example), and set another screw or nail. (For accuracy, the pins should be just outside the measured point.)
To draw the ellipse, align the pins and pencil along the vertical edge of the workpiece. While keeping the pins tight to the plywood edges, move the bottom pin (the rise) to the right as the top pin (the run) descends the vertical.
Use a grid
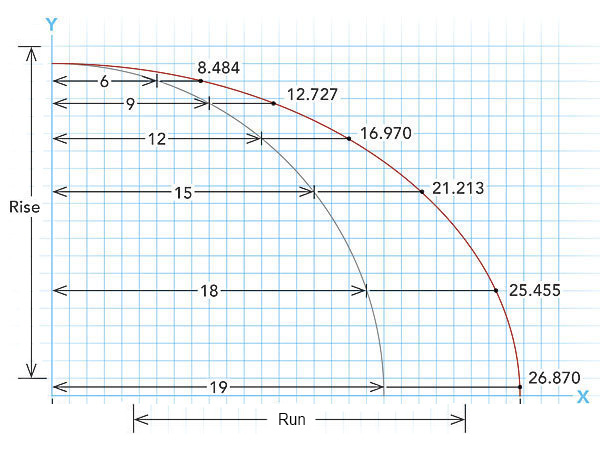
If an ellipse is too big to lay out with a trammel, it can be drawn using an algebraic formula. Begin by drawing a grid on an appropriately sized piece of paper, a sheet of plywood, or the subfloor. If you divide the horizontal axis into 20 parts, you’ll be plenty accurate. To draw the companion hip or valley to a curved common rafter, you’ll want first to draw the common. For the sake of illustration, we’ll use a quarter radius to describe the common, which can be drawn by swinging an arc from the intersection of the x axis and y axis. The elliptical hip or valley is laid out as an extension of the common, in a ratio of 12:17. On the grid, although each unit of rise remains the same, every 12 in. of run gets stretched to 17 in. to describe regular hips or valleys. To elongate the radius into an ellipse, multiply each point on the x axis (which represents the run) by the square root of 2, which is 1.414. The y axis (representingthe rise) stays the same.
After the coordinates are laid out, tack a flexible strip of wood at each point of the stretched grid to describe the elongated curved line. Now the ellipse can be transferred onto the stock.
Top photo: courtesy of Architectural Resources Group Inc. Inset photo: David Wakely. Drawings: Rodney Diaz.
Fine Homebuilding Recommended Products
Fine Homebuilding receives a commission for items purchased through links on this site, including Amazon Associates and other affiliate advertising programs.

Leather Tool Rig

Stabila Classic Level Set

Peel & Stick Underlayment





View Comments
A video demonstration detailing each ellipse technique would be very helpful.
Wow, that was complicated. How about measuring half the run from the height point back to the run plane, on both sides of the midpoint. That will give you your focal points. No reason to make it confusing.
Why 12 and 17? Would other ellipses work as well? Is there a structural reason for that particular ellipse?